As I read through Jo Ann’s last post about Example 9 from the book. I loved the connections to questioning and discourse that she developed. Example 9- ‘More Than Meets the Eye’ is definitely an opportunity for students to explore, predict, justify, check, and repeat/refine. I don’t know many students, who would move through this problem smoothly and without having to think through the problem, discuss it with peers, offer some thoughts, and go back to the drawing board. It is the kind of problem that I think we need to be asking all of our students, and especially higher level ones.
As I thought about the processes involved in this one encounter, it made me look at examples 5 and 6 much more carefully. How could we use these kinds of interactions to build a student’s capacity to tackle the problem in example 9?
I like the progression that these two problems are showing as Example 6 (Distribute Thoroughly) has a first year algebra student analyzing the errors a peer made in the multiplication of
It is a nice early step in having students Construct viable arguments and critique the reasoning of others. The student isn’t asked to find the right answer, they are asked to analyze the situation to identify where the problem went wrong, offer clarification, and help the peer understand the process more clearly. It is a great example of asking a different question to take the focus off of just finding the answer.
Example 6 is not nearly as complicated as example 9 (it’s not an accident, I’m sure), but it does illustrate the point that if we want students to be able to construct viable arguments, they need to start somewhere, they need to start today, and they don’t have to be complicated problems. Look at the kinds of problems we are already doing and let’s see if we can’t ask different questions about them.
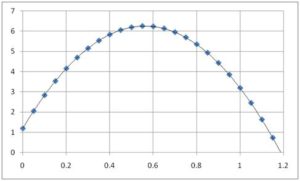
I love Example 5-‘Horseshoes in Flight’ for its simplicity, as well. It’s a simple free falling body quadratic application using a horseshoe (I like bowling balls, or potato cannons they seem to generate a lot of interest); used with algebra 2 students in this case (although I do think this could be done with late algebra I students in some cases). The nuance is in the question being asked. It wasn’t just create or use the model, but analyze the different forms of the model to identify the equation that is most useful for finding the maximum height of the horseshoe.
The question itself is very simple, but note in the Classroom description that the group report centered on analyzing all four equivalent forms for the information each one was able to offer. Yes, that’s it! Don’t only recognize that there is one form that you force everything to go through but be flexible in working with multiple forms of any equation, get used to discussing equivalent forms of equations, and recognize that each has value and an application.
Multiple Forms/Approaches
Jo Ann and I often work with algebra I teachers who only teach one form of the equation because students may struggle with remembering slope intercept, point slope, standard, or (god forbid) two-point form. I think the issue isn’t can they remember each form but are we asking the right kinds of questions that allow students to analyze situations to identify the best form for each set of conditions. I think example 5, models this kind of thinking.
A couple of Quick Notes that came to mind as I read and reread this post, and Jo Ann’s:
Multiple representations in 2 or the 3 examples helped students make connections and justify their conjectures.
Asking questions that move beyond what is the answer was central in all 3 examples and is the only way (perhaps that’s a big strong, but I’m staying with it) we are going to increase our students reasoning and sense-making.
and perhaps the most subtle point of all, use technology to take advantage of the power that exists in them. In example 9, the teacher could have asked the student to factor the expression 
but he didn’t. He asked the student to use his CAS (computer algebra system) to factor the expression and analyze the results. The student has enough information if we want to make him do it by hand but that isn’t the important skill in this example. This problem is about making connections, making mindful manipulations of symbolic representations, and reasoning with functions. In this problem the student graphed the equations, factored using an application, and discussed the mathematics at a very high level!