Just before the pandemic, I was given an incredible opportunity to spend some time with a brilliant group of 8 and 9 year old students. Our collective goal was to simply learn from each other during a mathematics lesson that I designed. Though the teacher and I met briefly before my visit, she did not require or ask that I address any specific content.
But first, a little about me. Having taught grades one through eight and also mathematics methods to pre-service teachers, I am no stranger to the classroom. In my current position at CTL, I continue teaching and learning mathematics but also have the opportunity to see K-12 classrooms and work with K-12 teachers throughout the state.
At the conclusion of the lesson with my new 3rd grade friends, I promised to one day write about them. Writing about their thinking was just one of the invitations I extended to the students that day so it was only fair that I agreed to also write. In the text that follows, I will share the lesson as I experienced it with the students. In writing about the work that the students and I did together, I am able to reflect on my own teaching but also share the remarkable ways in which these young students engaged with mathematics. My approach to writing the details of the day is strengths-based. Rather than point to or focus on deficiencies, I studied student work to uncover what the students could do.
The Invitation
I started the lesson by wishing the students a “Happy Palindrome Week”! I typically try to find and share interesting or fun math I find in the news, where appropriate, because it helps students see math outside of school and also provides opportunities for students to make connections. The students were eager to point out examples of palindromes they knew or had seen (Bob, wow, 303, etc.)
I combined the two routines of Notice and Wonder with Would You Rather for the bulk of our class time. Students were first invited to share their observations and questions about the displayed visual representing vehicles in line at the gas station. The gas station context was chosen intentionally for this age group. Standing in line and waiting your turn is a big deal in third grade!
The original task linked here invites students to choose line A or line B after studying two lines of vehicles at the pump. However, I chose to start the task instead by displaying only the drawing, so that there were no words or numbers. This opened the task up for more discussion and participation by all students. I wanted to intentionally keep students from grabbing the numbers and begin operating so that they could first make sense of the problem. Another benefit of this approach was that it naturally built interest and students were more apt to stay with their work until the end.
As the students shared their observations and questions, I gradually revealed words and numbers until all of the needed information was visible. For example, “back of the line” or “car” labels and each box that represented a vehicle displayed a number indicating its fuel capacity. The students and I agreed that the gas nozzle would reach either side of the vehicles. Some students aptly mentioned that the gas tanks “may not be all the way empty”. However, we chose to let that distinction go for this lesson.
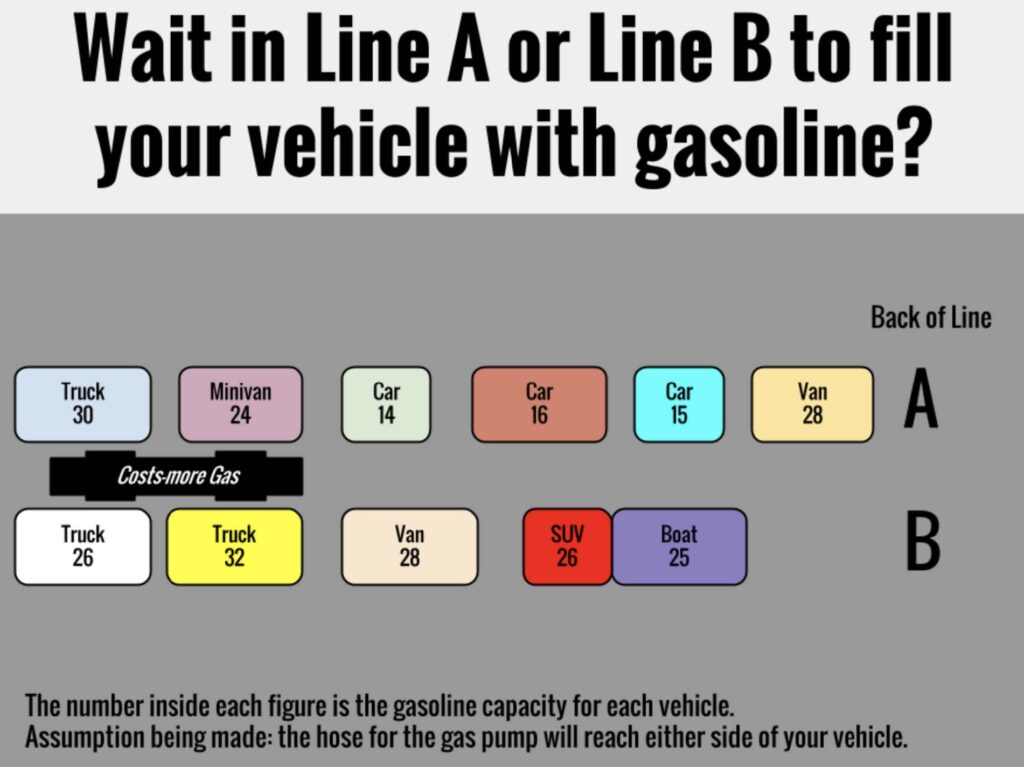
The students were asked to choose which line they would rather get in if they were going to fill up on gasoline. Included in the work, students were asked to eventually share their decisions, including the mathematics they used and their reasoning, with the class. Finally, students had the opportunity to question each other and then revise their thinking after hearing from other groups.
The groups of four had a large piece of paper so that each student had ample space for their words, pictures, numbers, and/or symbols. Pencils, rulers, counters, hundreds charts, and other typical classroom tools were also available for student use. I would have allowed student use of calculators, had I gotten any requests.
Engaging with Mathematics and Student Approaches to Addition
The students were eager to get started and quickly left the gathering area to join their groups. Student talk filled the room as they shared ideas. Group dynamics are always interesting to observe, and this class was no exception. Some students busied themselves with gathering additional supplies, some students began drawing, and others watched as they contemplated where to start. Some groups wanted to have each member do their work independently while other groups wanted to decide together what to do and then have one person record the work.
As shown below, this group worked very hard, and made sure to label member’s contributions.
As shown in the student work sample, there is great variety in how students made their decision regarding which line they would choose. In spite of the wide variety in how students arrived at their decision, most groups demonstrated that they thought the capacity of each tank should be added in order to arrive at a total. Not all groups arrived at the correct totals, but the students did unanimously choose to get in Line A, even though it had more cars. Students correctly concluded that the length of the line is not the determining factor but instead it is the total fuel capacity of the vehicles in line.
Place value knowledge was demonstrated by several students. Some students represented each fuel capacity as ones and tens by placing a tick or dot for each. The ten 1s were grouped with a circle and a ten was added to the appropriate column and then ten 10s were grouped and a hundred was drawn. For example, student work in Figure 1 and Figure 2 show Line A’s fuel capacity by representing each number, grouping, and arriving at 126. There is also evidence of work with ten frames and an understanding of tally marks as shown by two other group members in Figure 1.
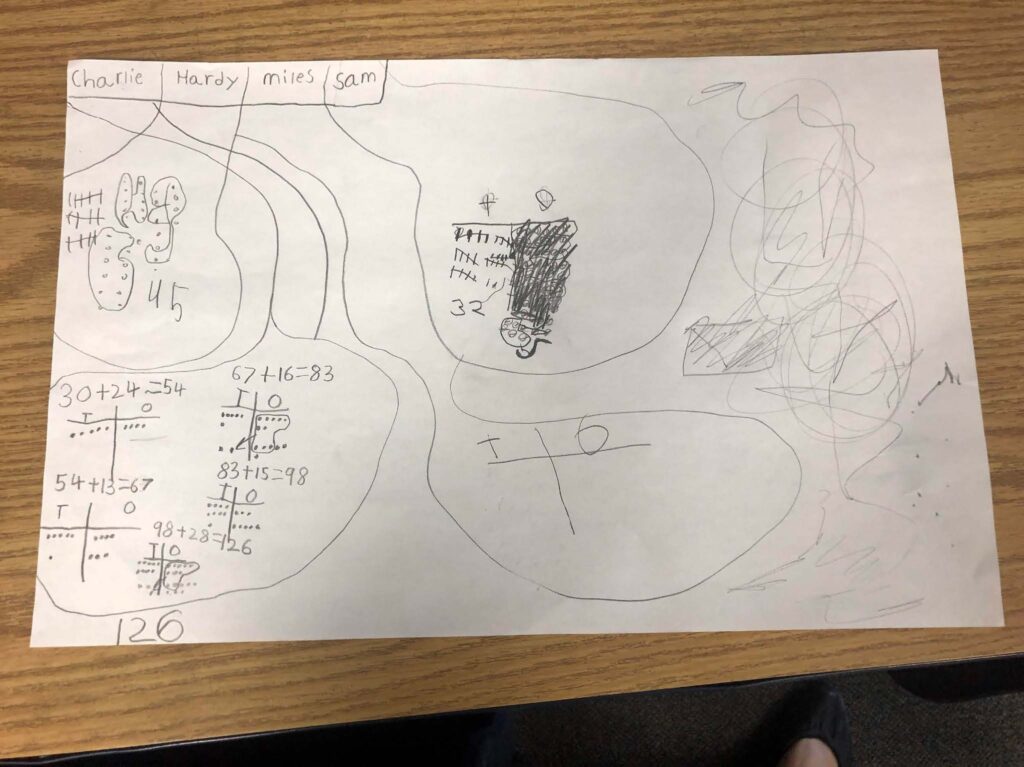
Also seen in Figure 2 is a different approach. Students chose to break numbers apart such as 26 into 20 and 6, to simplify the addition. This method shows some place value understanding as well as number sense.

Other groups of students recorded the ones digits vertically and added them mentally before adding to the total number of tens (100 + 26 = 126). This method is demonstrated in Figure 3.
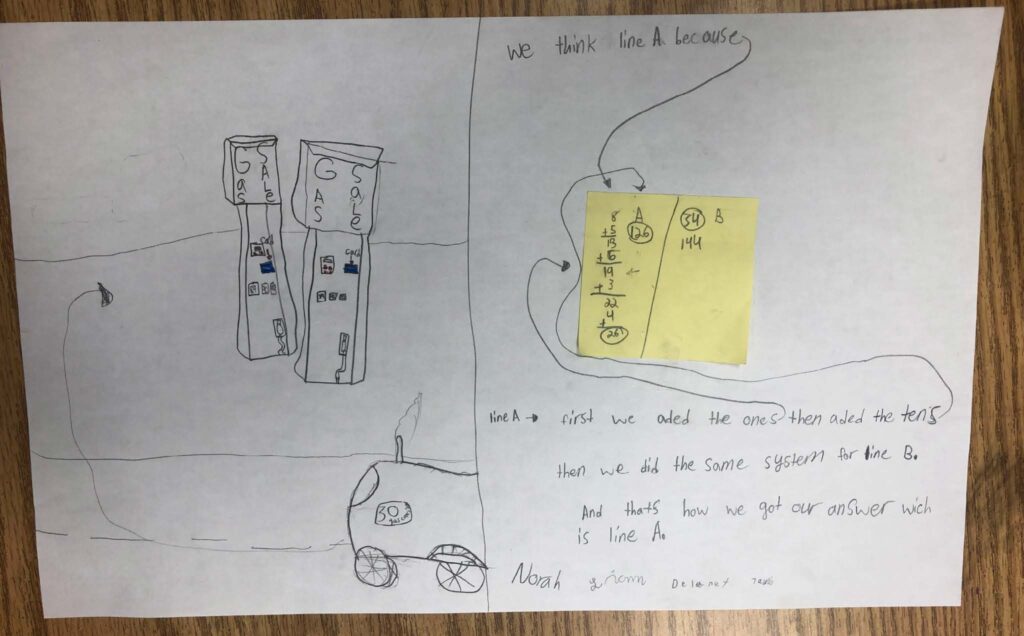
“B has less cars but more gas” was stated repeatedly by Allison and her group members, see Figure 4. Their addition appears to be mental and completed in a running total fashion. Students added two numbers at a time and then added the next number until all numbers were added. Though Allison’s group was correct in stating that Line A is “faster”, their calculations were off by ten gallons for Line B.

Aiden’s work, shown in Figure 5, also appears to show mental addition. Aiden added the numbers in the same order as they were presented and seems to have done his calculations at least twice. Nicole, who is also part of Aiden’s group, shows some attempts to break the numbers apart by tens (20 + 30 + 20 + 20 + 20) and ones (6 + 6 + 9 + 6 + 7) for Line B.
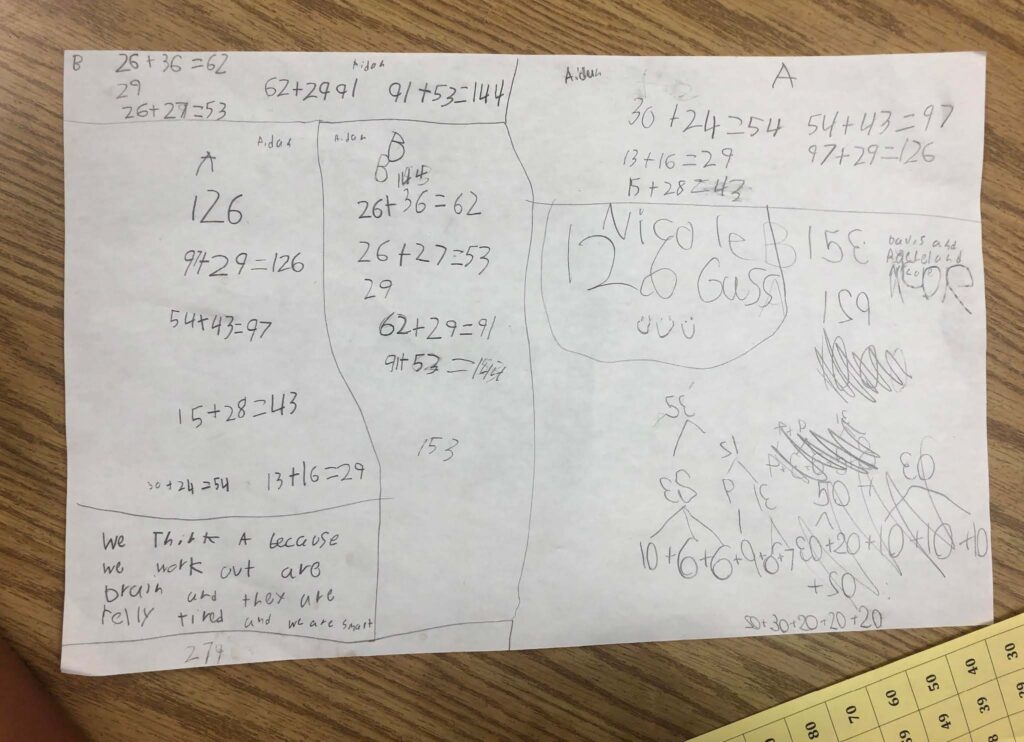
The students demonstrated a conceptual understanding of the meaning of addition and correctly compared the two amounts showing that Line A would be the shortest wait. There were errors in some of their calculations. Not all students were able to keep track of the amounts as the tables of tens and ones with dots, tally marks, and groupings show.
I enjoyed walking around to observe the students as they worked and wished I had recorded some of their rich conversations. As the students worked, I asked them questions to understand their thinking process and strategies and to foster their positive dispositions toward mathematics. To conclude the lesson, the students and I met again in the gathering area. They were invited to share their findings, ask questions of other members, and give final reflections. One student even seemed to declare mathematics was not needed when she commented, “I would rather go in line A because when I go in the shorter line it always takes longer.”
Looking at the collective body of work completed by these young students, I consider and acknowledge all that was accomplished in just 45 minutes of work. Students demonstrated growth mindsets and high levels of perseverance. Students communicated either verbally or in writing their understanding and mathematical processes. I am grateful for the opportunity to learn alongside each student that day and look forward to my next visit with young mathematicians.
